Table Of Content

At least half of the required front setback must be permeable and at least 20% of it must be unpaved and landscaped with plant material. Habitable rooms, excluding kitchens, home offices and media rooms, must have glazing that’s at least 8% of the floor area. Any exposure that is less than these dimensions will require the approval of a variance. State-law ADUs may not have to follow all of these requirements. In hallways and living and sleeping areas, the minimum ceiling height is 7.5 ft. In other rooms (like the bathroom and kitchen), the minimum ceiling height is 7 ft.
Building an ADU may change your occupancy codes
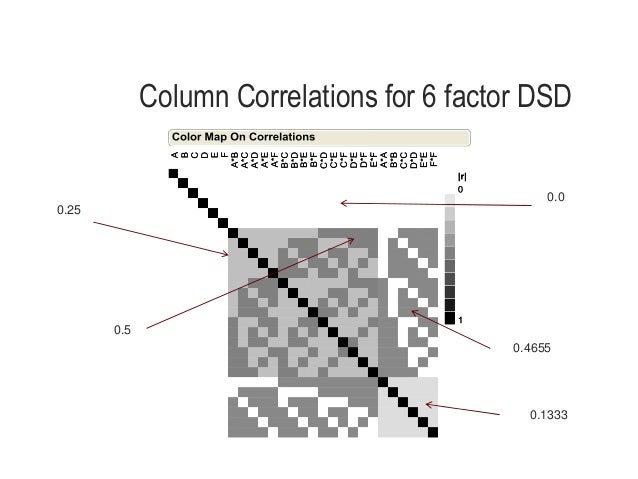
Due to their special structure however, DSDs can project to highly efficient response surface designs in the presence of sparsity in the number of active factors. Let us compare this design and plot to the standard screening design for eight factors. That design is the minimum aberration fractional factorial design. This design is in Table 2, which has one added center run to make both designs have 17 runs, including one center run.
Property requirements
This award is presented for the paper that has made the largest single contribution to the development of industrial application of quality control. This year’s winning paper was "A Class of Three-Level Designs for Definitive Screening in the Presence of Second-Order Effects." It was published in January 2011 in the Journal of Quality Technology. Copyright © 2024 Elsevier B.V., its licensors, and contributors. All rights are reserved, including those for text and data mining, AI training, and similar technologies.
Design of Experiments ( ,
That is, the runs of the design come in pairs that “mirror” each other. Suppose we encode the low setting of a factor as –, the high setting as +, and the middle setting as 0. Then, if one run of a foldover pair has factor settings encoded + 0 – + – +, the other run has factor settings encoded – 0 + – + –. Each pair of runs has one factor at its middle value and all the other factors at their high or low values. One run is at the center of the design region with all the factors at their middle setting.
Statgraphics Seminars
The exits and egress paths to the new units also must use protected wood frame construction, also called VA. After you decide to build an ADU, you must create architectural plans for your ADU. After the simulation is run, we want to count how many times the correct factors were retained in the models. We have been able to do this using the Stepwise platform, but for completeness, we would also like to be able to do it on the default Fit Definitive Screening Design platform. For more context, what we are trying to do is simulate new data for our outcome Y variable 1000 times, and we are looking to fit the DSD model for each simulation. The same critical parameters, Acid and Time, appear together with the less significant water spike.
Quantitative assessment and optimization of parallel contact model for flexible paddy straw: a definitive screening and ... - Nature.com
Quantitative assessment and optimization of parallel contact model for flexible paddy straw: a definitive screening and ....
Posted: Tue, 23 Jan 2024 08:00:00 GMT [source]
In addition, let us know if there are other topics that you would like to discuss. A response close to 95% is obtainable throughout the entire range of concentration. You can also see the effect of the interaction between catalyst and temperature, with the optimum value of one depending on the value of the other.
Characterization of a Biomanufacturing Fermentation Process Using a New DOE Approach: Definitive Screening Designs - BioProcess Insider
Characterization of a Biomanufacturing Fermentation Process Using a New DOE Approach: Definitive Screening Designs.
Posted: Sun, 03 Mar 2024 10:39:26 GMT [source]
In recent years, a class of experimental designs called "Definitive Screening Designs" have been developed that enable experimenters to fit a response surface model without doing additional runs. The initial set of runs has enough levels of each factor so that once insignificant factors have been eliminated, a second-order model with quadratic effects can be estimated in the remaining factors. Comparable in size to factorial experiments, they are a good alternative when curvature in the response variable is expected and the experimenter wants to avoid doing a second set of experimental runs. Statgraphics 18 includes definitive screening designs in its design catalog.
Related Projects
The engineers decide to use a definitive screening design that can estimate the square terms with 17 runs. Definitive screening designs include runs that are not in 2-level designs so that you can use definitive screening designs to estimate square terms. An example of a curved relationship is the amount of nitrogen in soil and the amount of fruit a plant produces. The addition of the right amount of nitrogen increases fruit production, but the addition of too much nitrogen decreases fruit production.
The analysis of DSDs often employ generic regression methods, which do not take advantage of all the useful structure DSDs possess. However, the analytical approach for DSDs proposed by Jones and Nachtsheim (2017), does take explicit advantage of the special structure of DSDs. Part 2 investigates all subsets of only those 2nd order terms containing the active main effects – referred to as obeying the heredity assumption. The effects listed in the two parts are finally combined to provide one model and analysis.
However, the addition of center points to these designs aliases all of the quadratic effects together. From a design with center points, you can assess whether the effect of at least 1 factor has a curved relationship with the response. However, you cannot distinguish any of the square terms from each other.
I still remember when Stu Hunter lectured to us in his course on DOE when I was an undergraduate engineering major. He began each lecture with a story about how he'd used what we were about to learn to help some company improve their processes. He had a unique knack for bringing real life into the classroom and encouraged many of us to pursue careers in statistics. If a bedroom is not fully enclosed, the adjacent room can count towards the light and ventilation requirements. The area must be at least 25 sq ft or 10% of the floor area of the room served.
However, since there are only 2 levels of each factor, it is impossible to estimate quadratic effects of the factors. Each two-factor interaction in the fractional factorial design is confounded with three other two-factor interactions. This means that if any two-factor interaction is active, the analysis can only indicate that there are four possible interactions that could explain the observed effect. Narrowing down this field to one interaction requires further experimentation. By contrast, the definitive screening design can reliably resolve any two-factor interaction that is large compared to its standard error.
By contrast, the definitive screening design can separately estimate the nonlinear effect of each factor. DSDs can also be considered as screening designs, since the number of terms to estimate in a full quadratic model, for example, is usually much larger than the number of tests. Traditional, Plackett Burman screening designs enable one to study main effects only, whereas Definitive Screening Designs can be used to study the effects of main effects as well as two factor interactions and quadratic effects. The purpose of screening is to separate the vital few factors that have a substantial effect on the response from the trivial many that have negligible effects. If a factor’s effect is strongly curved, a traditional screening design may miss this effect and screen out that factor. If there is a two-factor interaction, standard screening designs having a similar number of runs to the definitive screening design with the same number of factors will require follow-up experimentation to resolve the ambiguity.
We spent a lot of time in that class talking about screening designs. Screening designs are experiments that involve simultaneously changing the levels of many input factors, with the goal of identifying those "vital few" factors which have the greatest impact on the response variables. We talked a lot about 2-level factorial and fractional factorial designs. We even learned how to use Yates' Algorithm to calculate effects (this was when handheld calculators were just appearing). Stu taught us about interactions, confounding, half-normal plots, and various other analysis techniques that could help identify the important factors. We also learned how to augment the original experiment by adding additional runs to enable us to fit a real response surface model in whatever factors turned out to be important.
As with other resolution IV designs, it may be possible to sense the presence of 2-factor interactions but they will be very difficult to identify. The two-factor interactions have pairwise correlations that can take one of three values. The engineers use a screening design to determine which potential factors affect the output power for the cleaner.

No comments:
Post a Comment